Rails Again... Tracing Movements
By Neilor Tonin, URI  Brazil
Brazil
By Neilor Tonin, URI  Brazil
Brazil
Do you remember the railway station of PopPush City? If you don’t know about or only to remember, exist a railway station in an incredible hilly country. In addition, the station was built in last century and unfortunately, funds were extremely limited that time. It was possible to establish only a surface track. Moreover, it turned out that the station could be only a dead-end one (see picture) and due to lack of available space it could have only one track.
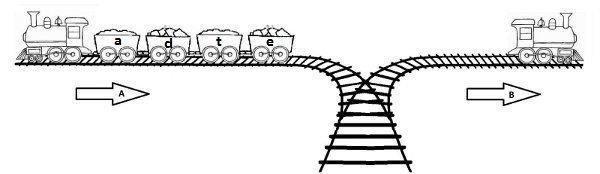
Every wagon arriving from the direction A continues in the direction B, reorganized in some way at the station. You can assume that every single wagon can be disconnected from the train before it enter the station and that they can move themselves until they are on the track in the direction B to be connected in the other locomotive. You can also suppose that at any time there can be located as many wagons as necessary in the station. But once a wagon has entered the station it cannot return to the track in the direction A and also once it has left the station in the direction B it cannot return back to the station.
All the wagons are identified by letters from a to z, all in lowercase. This means 26 wagons, at the maximum. The chief for train reorganizations must know what sequence of movements is needed to achieve a desired output order to continue going from station to B direction. The movements into the station and out of the station are described by the letters I and R (Insert and Remove respectely). Using the figure example, the input e,t,d,a and the desired output d,a,t,e, result in the movements I,I,I,R,I,R,R,R
The input consists of many test cases, where each one is a set of three lines. The first line is an integer number that represents the number of wagons. The second line contains the input sequence and a third line presents the desired output sequence. The last line of the input contains just 0, indicating the end of input.
The output file contains the lines corresponding to the number of test cases. Each line contain a sequence of I and R needed to produce the output. If it’s impossible ge nerate the I/R sequence, the message "Impossible" must be printed.
| Input Sample | Output Sample |
|
4 |
IIIRIRRR |