Lazy Jumping Frog
 Brazil
Brazil Brazil
BrazilMr. Frog lives in a grid-like marsh of rectangular shape, composed of equally-sized cells, some of which are dry, some of which are only watery places. Mr. Frog lives in a dry cell and can jump only from a dry cell to another dry cell on his wanderings around the marsh.
Mr. Frog wants to visit his girlfriend, Ms. Toad, who also lives in a dry cell in the same marsh. But Mr. Frog is lazy, and wants to spend the minimum amount of energy in his jumping way to Ms. Toad’s home. Mr. Frog knows how much energy he spends in any of his jumps. For any single jump, Mr. Frog always uses the following figure to determine which are the possible target cells from his current position (the cell marked F), and the corresponding energy spent in the jump, in calories. Any other cell is unreachable from Mr. Frog’s current position with a single jump.
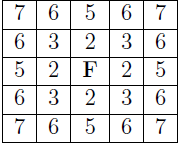
Your task is to determine the minimum amount of energy that Mr. Frog needs to spend to get from his home to Ms. Toad’s home.
The input contains several test cases. The first line of a test case contains two integers, C and R, indicating respectively the number of columns and rows of the marsh (1 ≤ C, R ≤ 1000). The second line of a test case contains four integers Cf, Rf, Ct, and Rt, where (Cf,Rf) specify Mr. Frog’s home location and (Ct,Rt) specify Ms. Toad’s home location (1 ≤ Cf, Ct ≤ C and 1 ≤ Rf, Rt ≤ R). The third line of a test case contains an integer W (0 ≤ W ≤ 1000) indicating the number of watery places in the marsh. Each of the next W lines contains four integers C1, R1, C2, and R2 (1 ≤ C1 ≤ C2 ≤ C and 1 ≤ R1 ≤ R2 ≤ R) describing a rectangular watery place comprising cells whose coordinates (x, y) are so that C1 ≤ x ≤ C2 and R1 ≤ y ≤ R2. The end of input is indicated by C = R = 0.
For each test case in the input, your program must produce one line of output, containing the minimum calories consumed by Mr. Frog to go from his home location to Ms. Toad’s home location. If there is no way Mr. Frog can get to Ms. Toad’s home, your program should output impossible.
| Sample Input | Sample Output |
|
4 4 |
14 |