Entangled Ropes

Four children are playing holding two ropes. Initially, the children are positioned in the four corners of a square, numbered 1 to 4 as shown below:

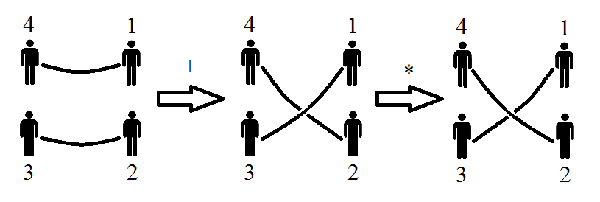
In the beginning of the play, the children in positions 1 and 4 hold a rope, and the children in positions 2 and 3 hold the other rope. Then the children perform a sequence of movements that can be of three types:

• Movement + : Children in positions 1 and 2 switch places, and the child at position 2 pass the rope over the child at position 1.
• Movement - : Children in positions 1 and 2 switch places, and the child at position 1 pass the rope over the child at position 2.
• Movement * : Children rotate clockwise. Who is in the position 1 goes to position 2, who is in position 2 goes to position 3, who is in position 3 goes to position 4, and who is in position 4 goes to position 1.

You must develop a program to predict the end of the game: After a given sequence of movements, do the ropes can be completely separated as they were initially without the children change places?

John Conway is one of the children participating in the game. He is a very smart boy and decided to give you a hint to solve the problem: after the sequence of movements, the ropes can not be completely separated if and only if the sequence of movements is equivalent to a sequence of alternating movements. A sequence of movements is alternating if it switches the '+' and '-' movements between a movement of '*', using the format "+++...+++*---...---*+++...". For example, "+++", "-*++*-" and "+++*----*" are alternating sequences. An alternating sequence is always started by a movement of '+' or '-', and don't have consecutives "*" movements, so sequences "*---*++" and "++**-" not are alternating. The sequence "+-++*+" is not alternating, but is equivalent to the alternating sequence "+*-*", because the two sequences leave the two ropes in the same situation.