Hyperfield
By Maratona de Programção da SBC, ACM ICPC 2017  Brazil
Brazil
By Maratona de Programção da SBC, ACM ICPC 2017  Brazil
Brazil
Two anchors are given, two points A = (XA , 0) and B = (XB , 0), forming a horizontal segment, such that 0 < X A < XB, and a set P of N points of the form (X, Y), such that X > 0 e Y > 0. The leftmost figure exemplifies one possible input.
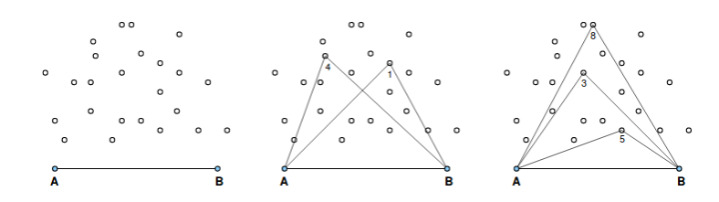
To "connect" a point v ∈ P we need to draw the two line segments (v, A) and (v, B). We want to connect lots of points, but in such a way that the segments intersect only at the anchors. For example, the middle figure shows two points, 1 and 4, which cannot be connected at the same time, because there would be intersection of the segments outside the anchors. The rightmost figure shows that it is possible to connect at least 3 points, 8, 5 and 3, with intersection only at the anchors.
Your program should compute the maximum number of points that it is possible to connect with intersection of segments only at the anchors.
The first row of the entry contains three integers, N (1 ≤ N ≤ 100), XA and XB (0 < XA < XB ≤ 104), representing, respectively, the number of points in the set P and the abscissae of anchors A and B. The next N rows each contain two integers Xi and Yi (0 < Xi , Yi ≤ 104), representing the coordinates of the points, for 1 ≤ i ≤ N. There are no coincident points and no two distinct points u and v such that { A, u, v } or { B, u, v } are collinear.
Your program should print a line containing an integer, representing the maximum number of points of P that can be connected with segment intersection only at the anchors.
| Input Samples | Output Samples |
|
4 1 10 2 4 5 1 6 5 7 8 |
3 |
|
2 2 8 3 4 7 4 |
1 |